Tangen (bahasa Belanda: tangens; lambang tg, tan) dalam matematika adalah perbandingan sisi segitiga yang ada di depan sudut dengan sisi segitiga yang terletak di sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90o). Perhatikan segitiga di kanan; berdasarkan definisi tangen di atas maka nilai tangen adalah

Nilai tangen positif di kuadran I dan III dan negatif di kuadran II dan IV.
Hubungan Nilai Tangen dengan Nilai Sinus dan Cosinus
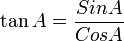
Nilai Tangen Sudut Istimewa







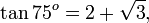

Kotangen
Kotangen (lambang: cot, cotg, atau cotan) dalam matematika adalah perbandingan sisi segitiga yang terletak pada sudut dengan sisi segitiga yang terletak di depan sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90o). Perhatikan segitiga di kanan; berdasarkan definisi kotangen di atas maka nilai kotangen adalah

Hubungan kotangen dengan tangen:
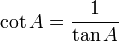


Tidak ada komentar:
Posting Komentar